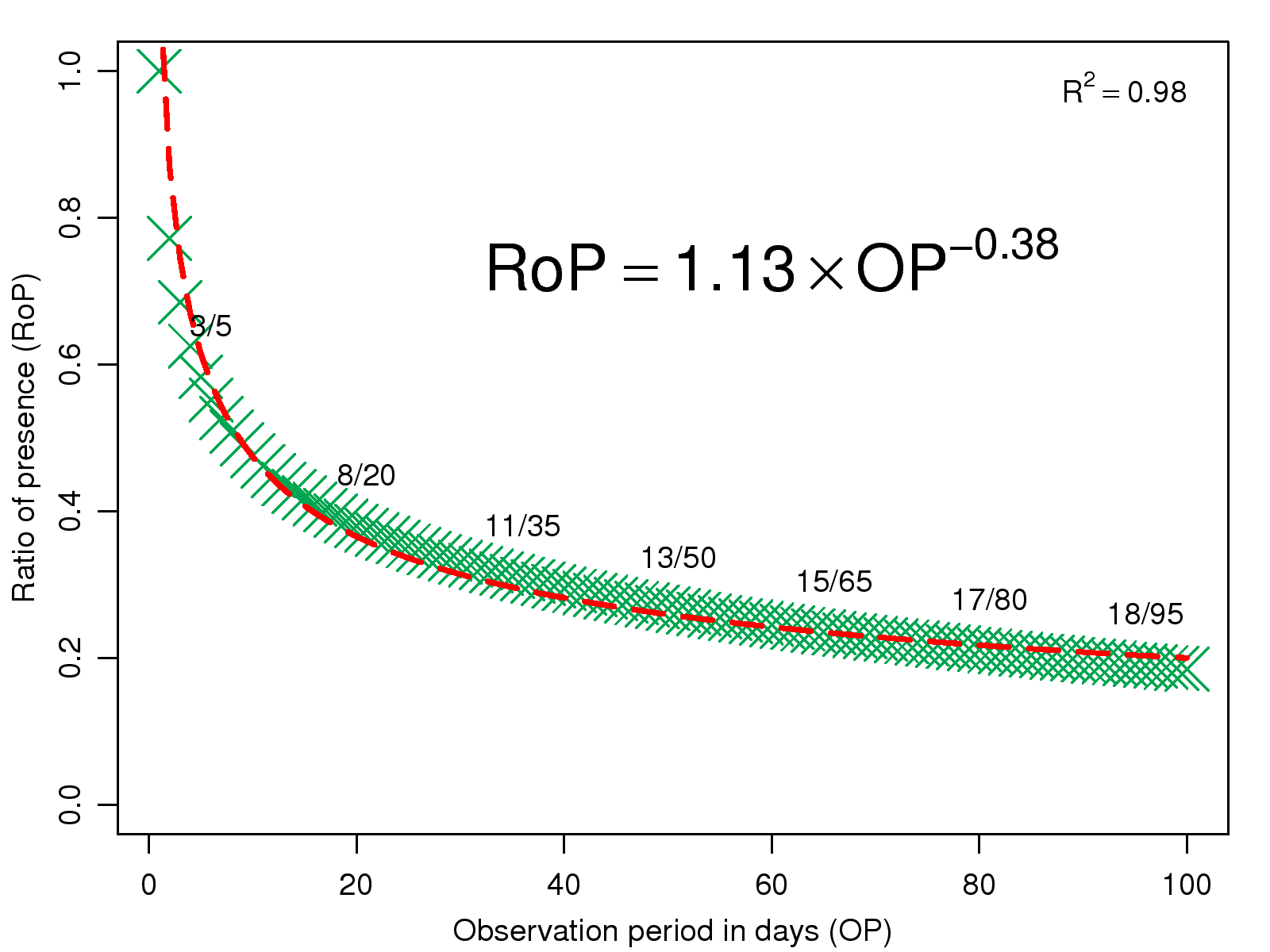
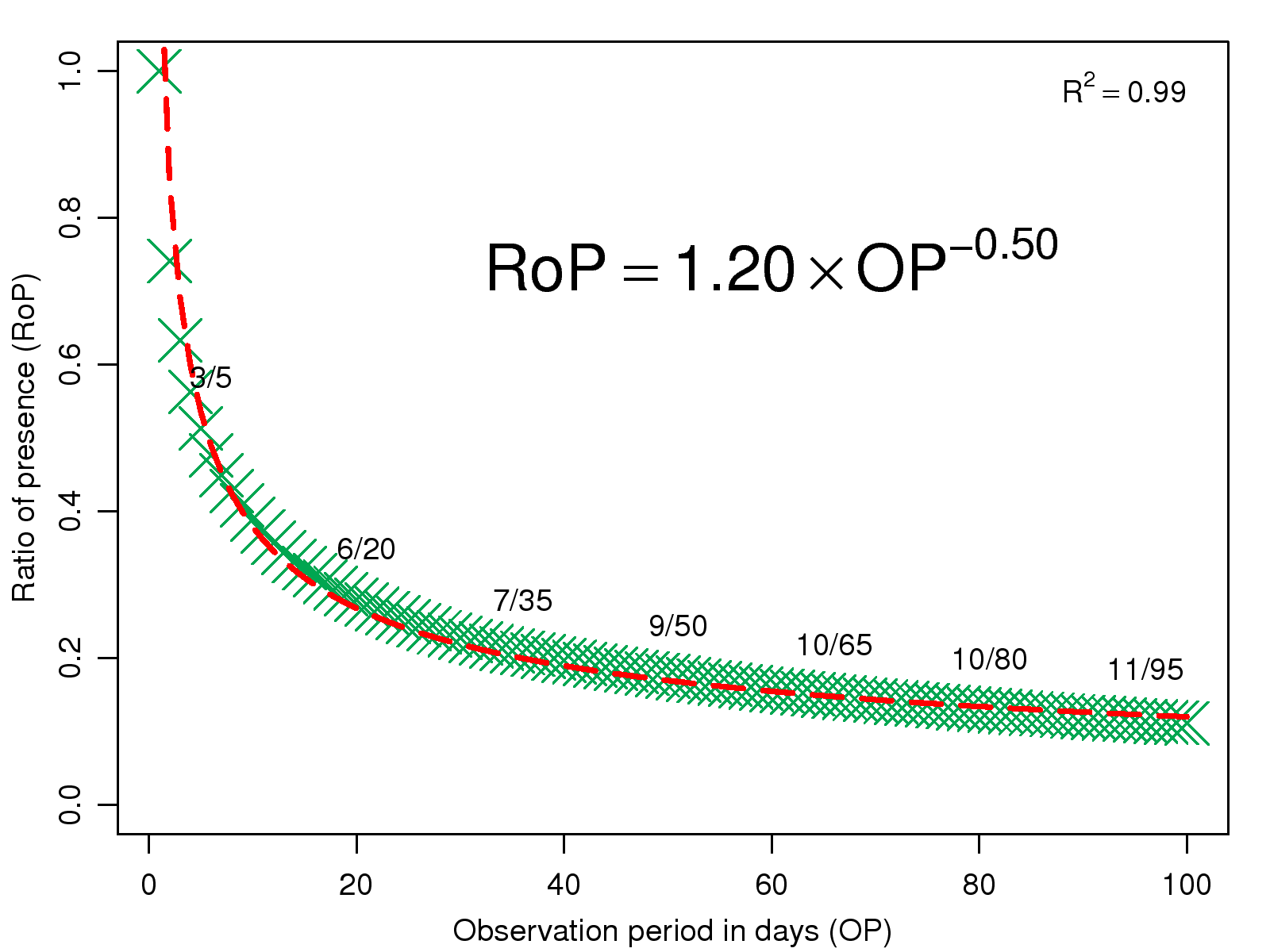
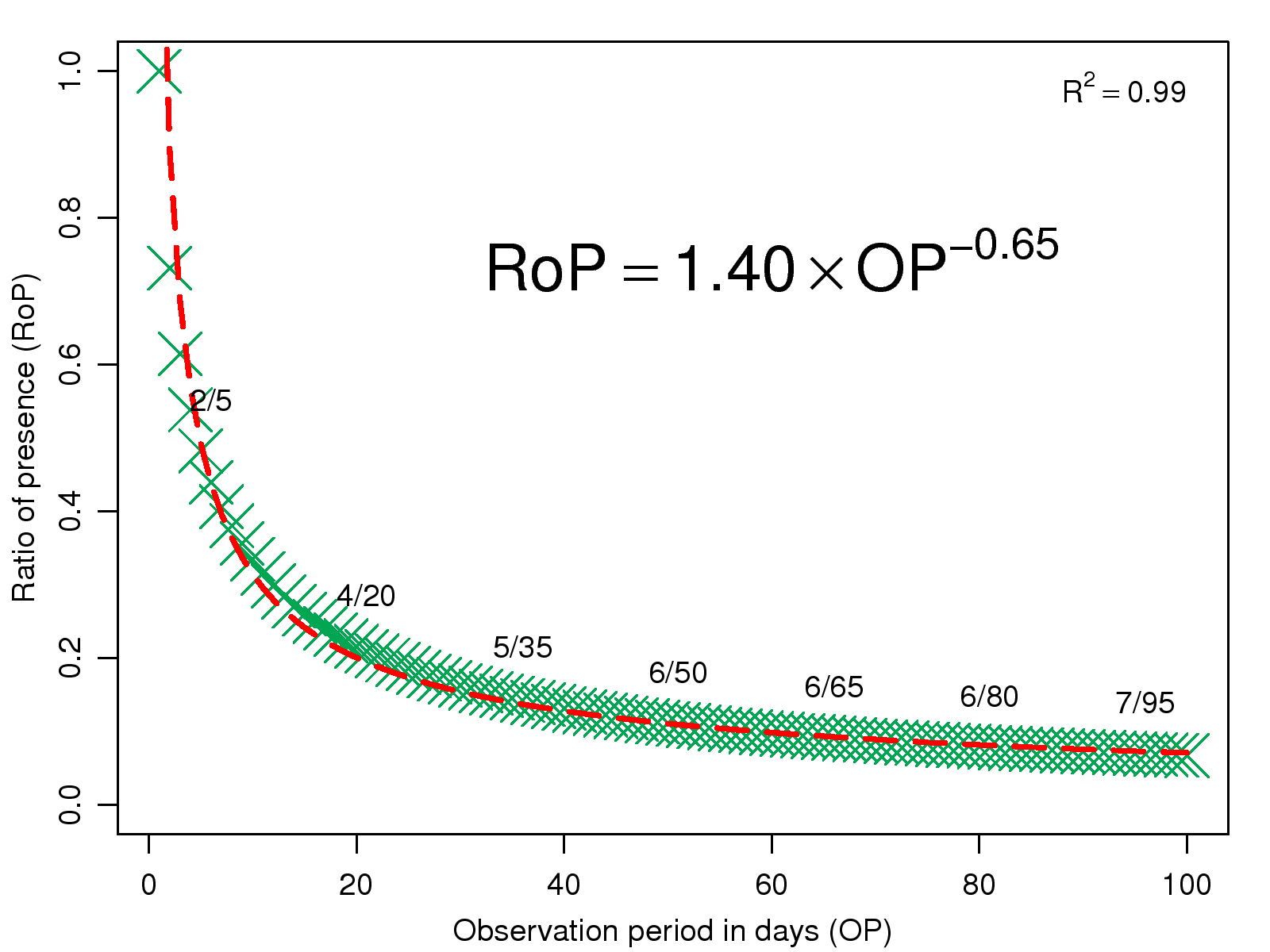
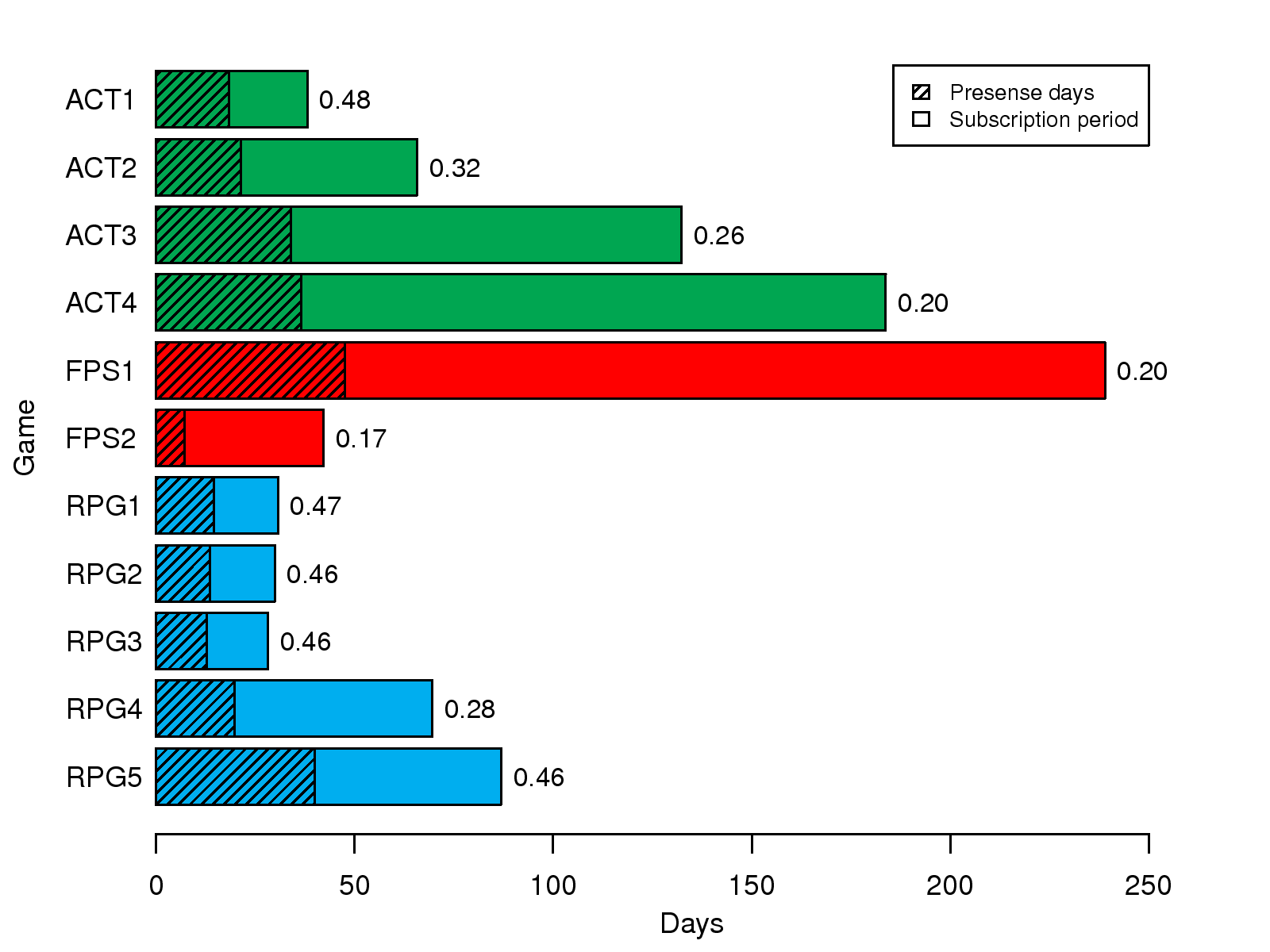
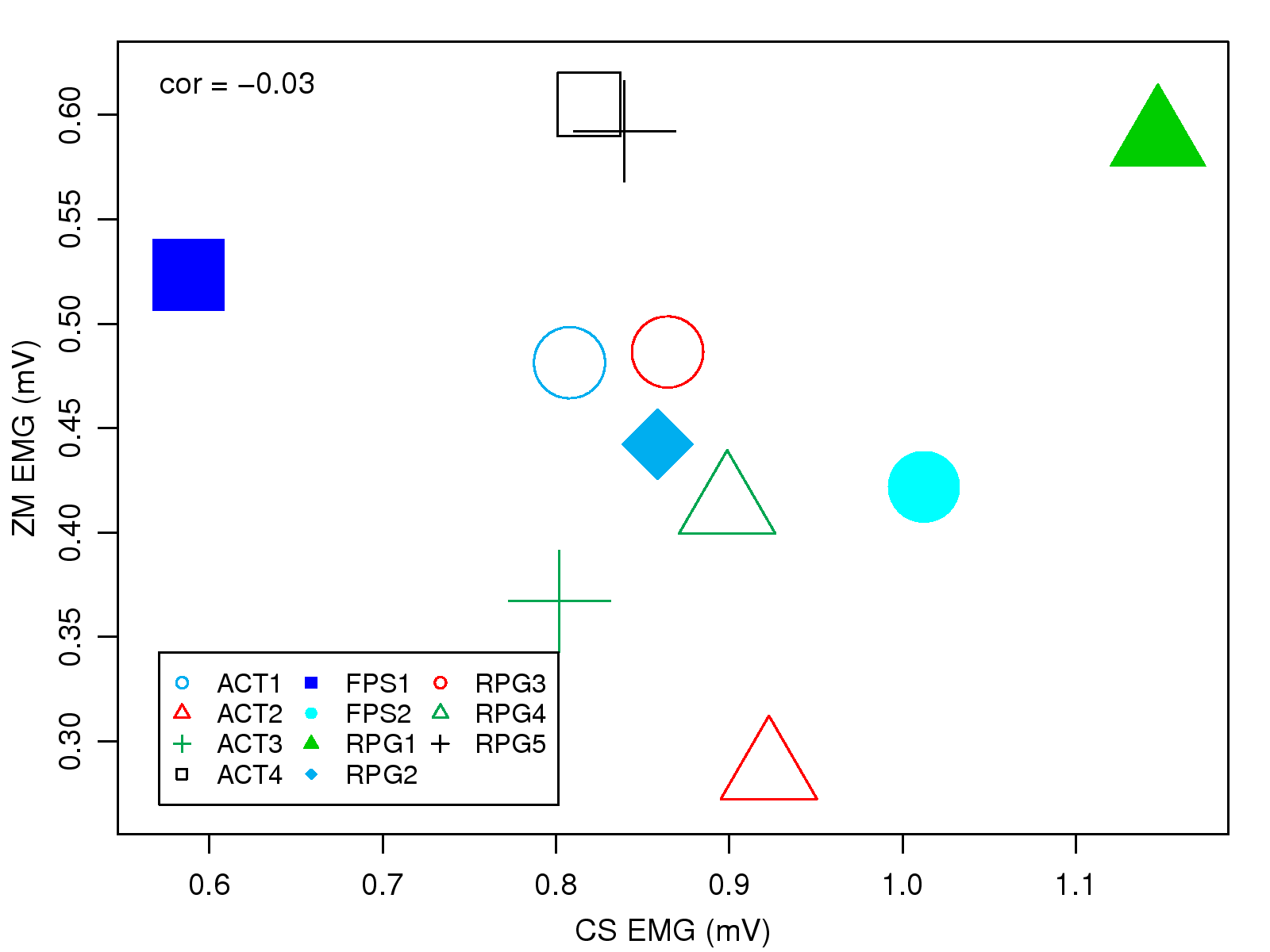
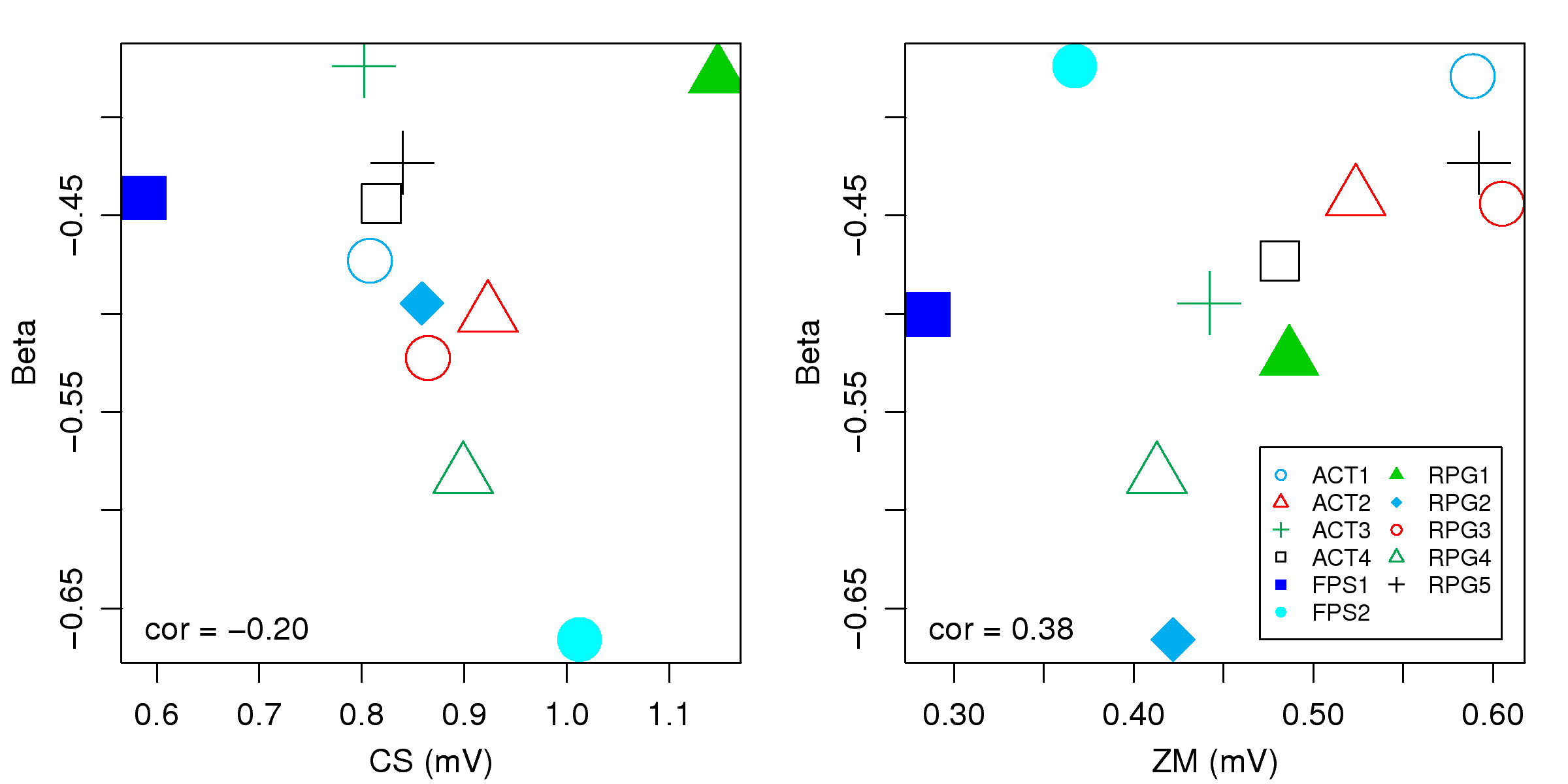
Table 3: The average strength of subjects' negative emotion
(CS) and positive emotion (ZM) during gameplay.
[1]
V. Lehdonvirta, "Virtual item sales as a revenue model: identifying attributes
that drive purchase decisions,"
Electronic Commerce Research, vol. 9,
pp. 97-113, 2009.
[2]
P.-H. Tseng, N.-C. Wang, R.-M. Lin, and K.-T. Chen, "
On The Battle between Online Gamers and Lags," in
Proceedings of IEEE CQR 2011, May 2011.
[3]
K.-T. Chen, J.-W. Jiang, P. Huang, H.-H. Chu, C.-L. Lei, and W.-C. Chen,
"
Identifying MMORPG Bots: A Traffic Analysis Approach,"
EURASIP
Journal on Advances in Signal Processing, 2009.
[4]
N. Ravaja, T. Saari, M. Salminen, J. Laarni, and K. Kallinen, "Phasic
emotional reactions to video game events: A psychophysiological
investigation,"
Media Psychology, vol. 8, no. 4, pp. 343-367, Nov.
2006.
[5]
N. Ravaja, M. Turpeinen, T. Saari, S. Puttonen, and
L. Keltikangas-Järvinen, "The psychophysiology of james bond: Phasic
emotional responses to violent video game events."
Emotion, vol. 8,
no. 1, pp. 114-120, 2008.
[6]
L. E. Nacke, M. N. Grimshaw, and C. A. Lindley, "More than a feeling:
Measurement of sonic user experience and psychophysiology in a first-person
shooter game,"
Interacting with Computers, 2010.
[7]
H. Desurvire, M. Caplan, and J. A. Toth, "Using heuristics to evaluate the
playability of games,"
Proceedings of ACM CHI'04, Apr. 2004.
[8]
P. Sweetser and P. Wyeth, "Gameflow: a model for evaluating player enjoyment
in games,"
Computers in Entertainment (CIE), vol. 3, no. 3, Jul.
2005.
[9]
L. Nacke and C. A. Lindley, "Flow and immersion in first-person shooters:
measuring the player's gameplay experience," in
Proceedings of the
2008 Conference on Future Play, ser. Future Play '08, 2008, pp. 81-88.
[10]
R. L. Mandryk and M. S. Atkins, "A fuzzy physiological approach for
continuously modeling emotion during interaction with play technologies,"
International Journal of Human-Computer Studies, 2007.
[11]
J. T. Cacioppo, G. G. Berntson, and J. T. Larsen, "The psychophysiology of
emotion,"
Handbook of emotions, pp. 119-142, 2000.
[12]
A. Achaibou, G. Pourtois, S. Schwartz, and P. Vuilleumier, "Simultaneous
recording of EEG and facial muscle reactions during spontaneous emotional
mimicry,"
Neuropsychologia, vol. 46, no. 4, pp. 1104-1113, Jan.
2008.
[13]
Y.-T. Lee, K.-T. Chen, Y.-M. Cheng, and C.-L. Lei, "
World of Warcraft Avatar History Dataset," in
Proceedings of ACM Multimedia Systems 2011, Feb
2011.
[14]
P.-Y. Tarng, K.-T. Chen, and P. Huang, "
An Analysis of WoW Players Game Hours," in
Proceedings of ACM NetGames 2008, 2008.
[15]
D. Pittman and C. GauthierDickey, "Characterizing virtual populations in
massively multiplayer online role-playing games,"
Advances in
Multimedia Modeling, 2010.
[16]
C. Chambers, W.-c. Feng, S. Sahu, and D. Saha, "Measurement-based
characterization of a collection of on-line games," in
Proceedings of
the 5th ACM SIGCOMM conference on Internet Measurement. USENIX Association, 2005.
[17]
W. Feng, D. Brandt, and D. Saha, "A long-term study of a popular MMORPG,"
in
Proceedings of NetGames'07, 2007, pp. 19-24.
[18]
Y.-T. Lee, K.-T. Chen, H.-I. Su, and C.-L. Lei, "
Are All Games Equally Cloud-Gaming-Friendly? An Electromyographic Approach," in
Proceedings
of IEEE/ACM NetGames 2012, Oct 2012.
[19]
A. Drachen, L. E. Nacke, and G. Yannakakis, "Correlation between heart rate,
electrodermal activity and player experience in first-person shooter games,"
in
Proceedings of the 5th ACM SIGGRAPH Symposium on Video Games, 2010,
pp. 49-54.
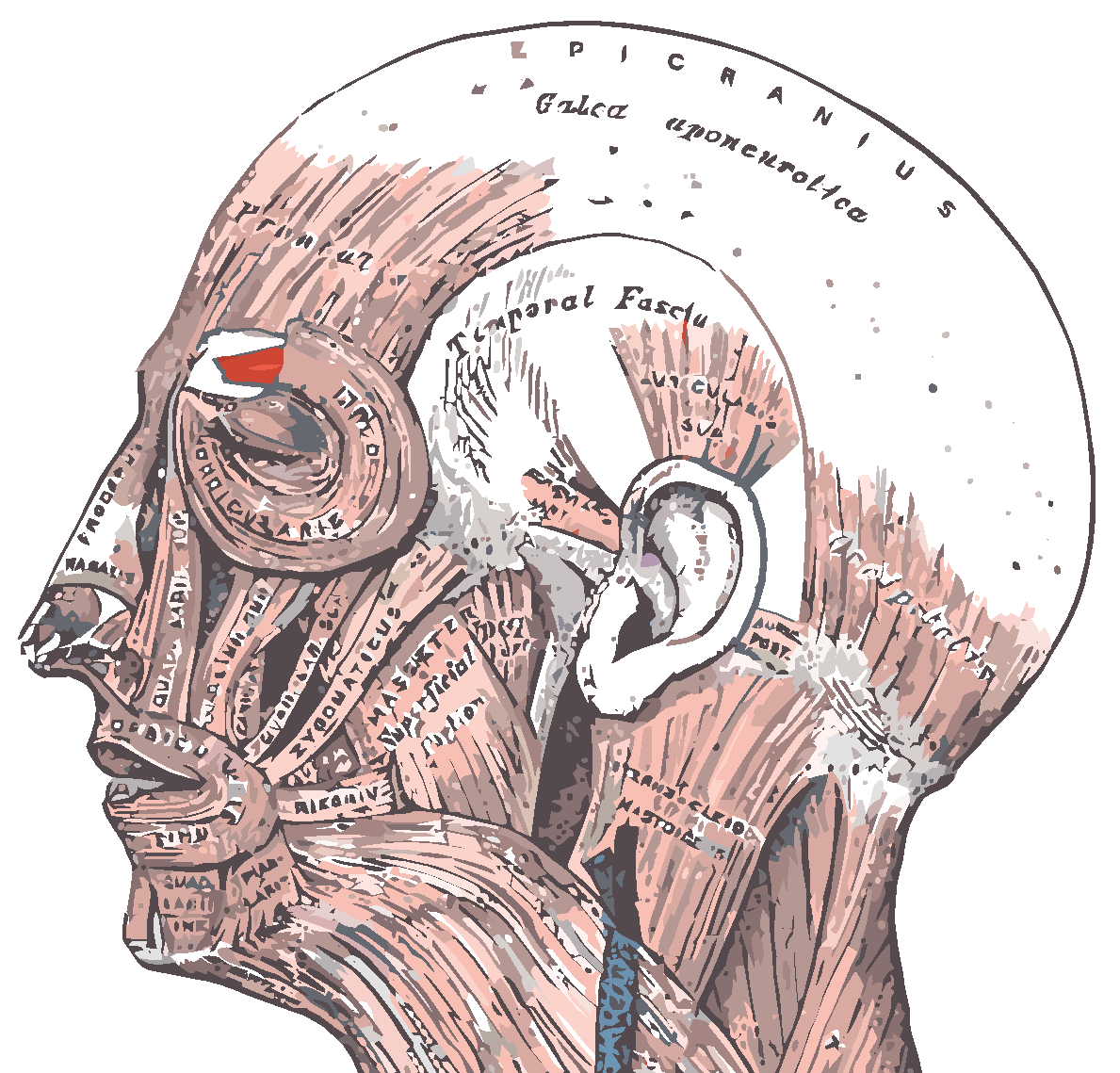 (a) Corugattor supercilli muscle
(a) Corugattor supercilli muscle
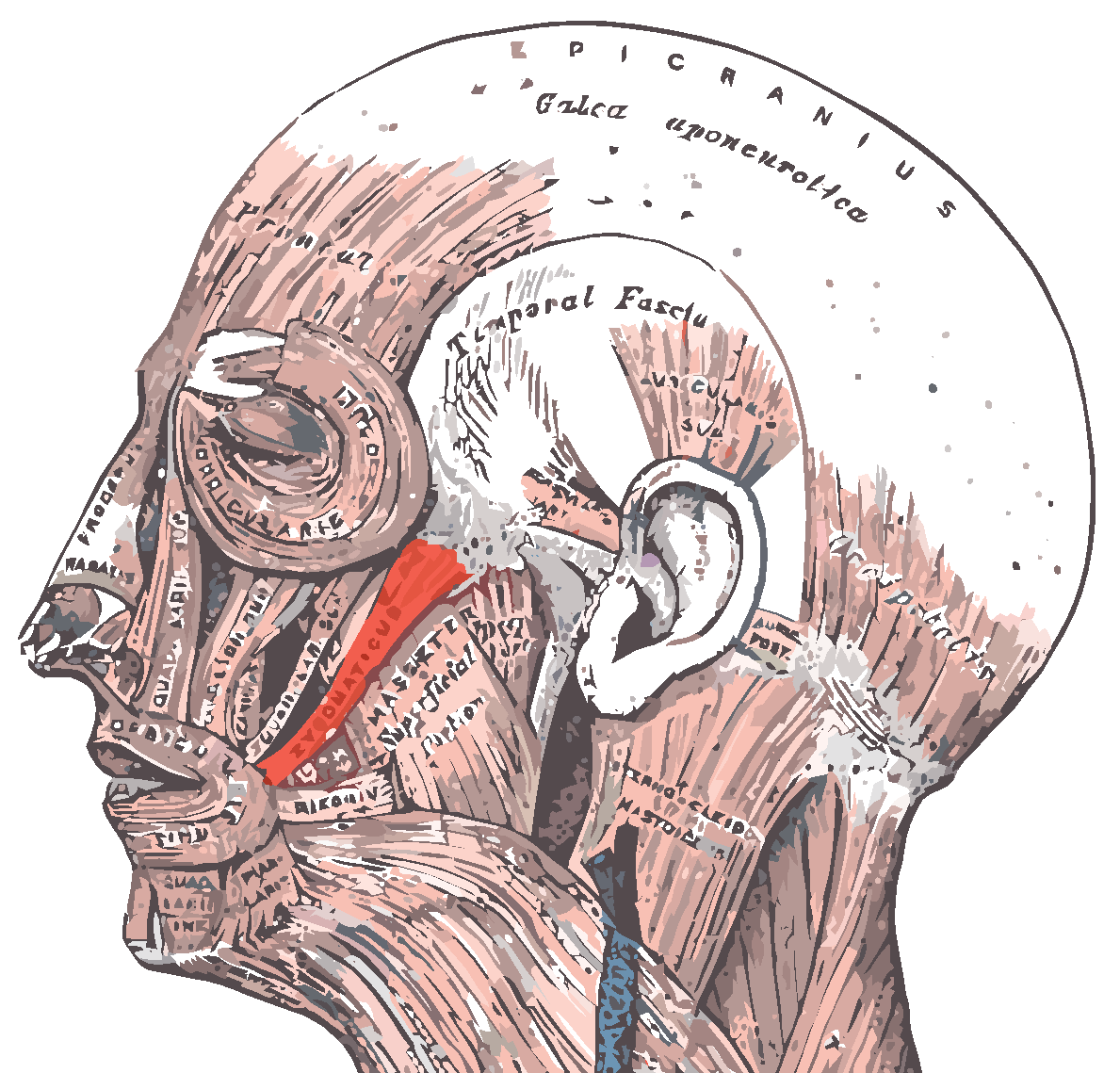 (b) Zygomaticus major muscle
(b) Zygomaticus major muscle