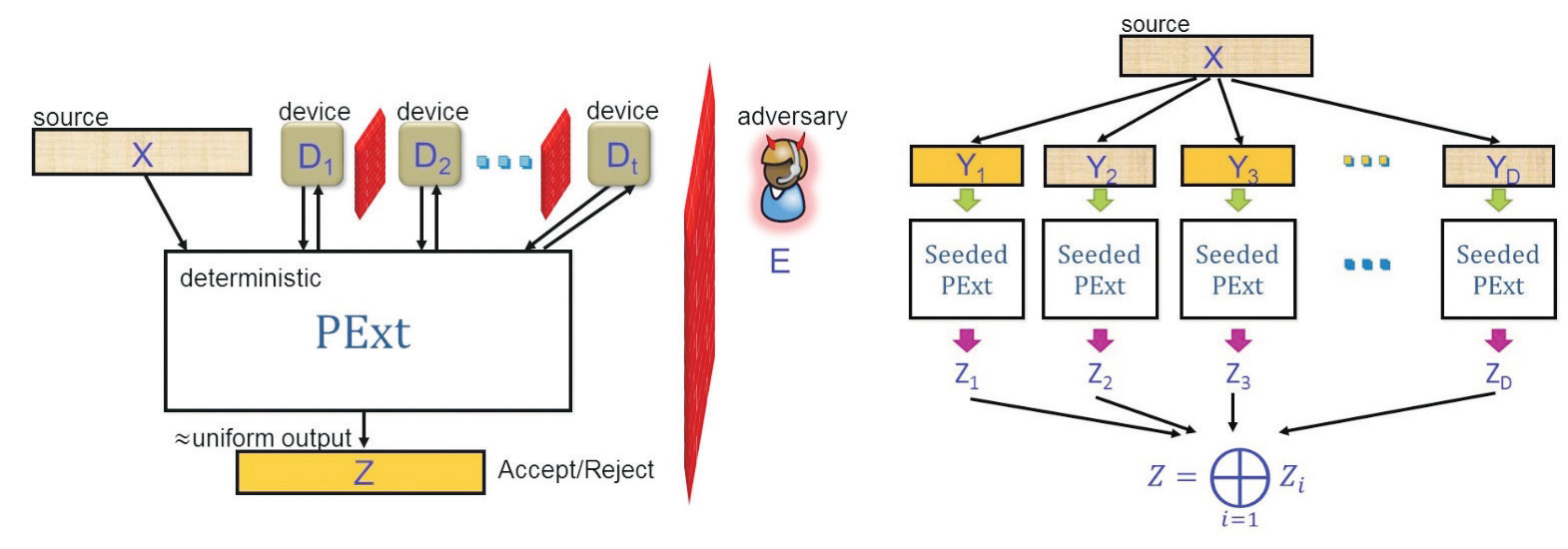
Physical Randomness Extractors: Generating CertifiedRandom Numbers with Minimal Assumptions
The 17th Conference on Quantum Information Processing (QIP 2014), February 2014
Kai-Min Chung, Yaoyun Shi, and Xiaodi Wu
- Institute of Information Science, Academia Sinica
Randomness is a precious resource pervasive in our daily life, but how can we be certain that any source of randomness is indeed truly random? Following literature in untrusted-device quantum cryptography, we propose a new framework of physical randomness extractor for extracting certifiable randomness from physical systems, combining ideas from cryptography, complexity theory, and quantum information. Our framework circumvents the hard-to-enforce independence or structure assumptions from existing solutions, and provably relies on minimal assumptions that can be based on the validity of physical laws. Specifically, we extract randomness from a set of untrusted non-communicating physical devices with the help of a single weak random source that is sufficient random to the devices. Our result also implies an optimal dichotomy theorem for experimentally certifying truly random events in physics.
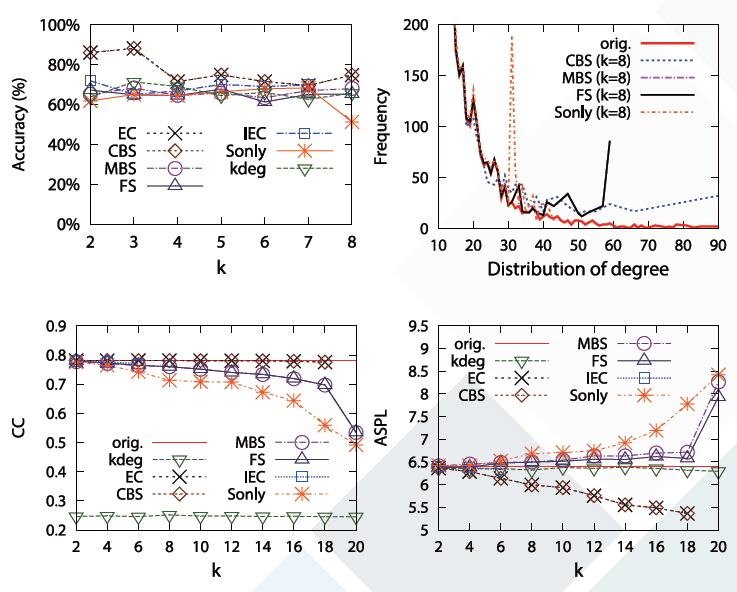
Structural Diversity for Resisting Community Identification in Published Social Networks
IEEE Trans. on Knowledge and Data Engineering 26 (2014): 235-252.
Chih-Hua Tai, Phillip S. Yu, De-Nian Yang, and Ming-Syan Chen
- Institute of Information Science, Academia Sinica
Vertex identification is one of the most important problems that have been addressed. This paper addressed a new privacy issue, referred to as community identification, as the community identity could represent the personal privacy information sensitive to the public, such as the political party affiliation. For this problem, we proposed the concept of structural diversity to provide the anonymity of the community identities. The k-Structural Diversity Anonymization (k-SDA) is to ensure sufficient vertices with the same vertex degree in at least k communities in a social network. We propose an Integer Programming formulation to find optimal solutions to k-SDA and also devise scalable heuristics to solve large-scale instances of k-SDA with different perspectives. The performances studies on real data sets from various perspectives demonstrate the practical utility of the proposed privacy schema and our anonymization approaches.