Reliable Multicast Routing for Software-Defined Networks
IEEE International Conference on Computer Communications, IEEE INFOCOM (2015).
Shan-Hsiang Shen, Liang-Hao Huang, De-Nian Yang, and Wen-Tsuen Chen
- Institute of Information Science, Academia Sinica
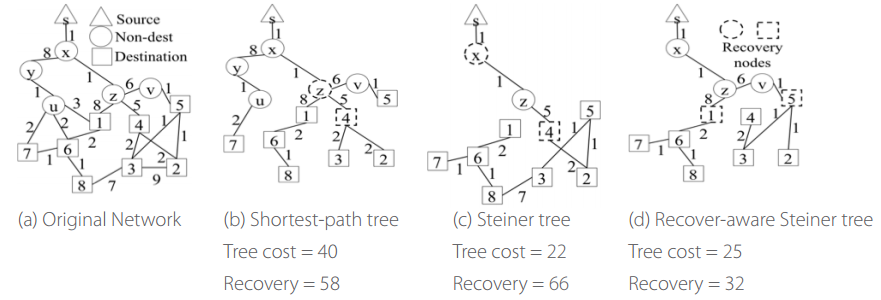
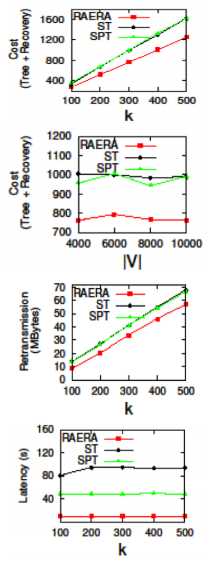
Current traffic engineering in SDN mostly focuses on unicast. By contrast, compared with individual unicast, multicast can effectively reduce network resources consumption to serve multiple clients jointly. Since many important applications require reliable transmissions, it is envisaged that reliable multicast plays a crucial role when an SDN operator plans to provide multicast services. However, the shortest-path tree (SPT) adopted in current Internet is not bandwidth-efficient, while the Steiner tree (ST) in Graph Theory is not designed to support reliable transmissions since the selection of recovery nodes is not examined. In this paper, therefore, we propose a new reliable multicast tree for SDN, named Recover-aware Steiner Tree (RST). The goal of RST is to minimize both tree and recovery costs, while finding an RST is very challenging. We prove that the RST problem is NP-Hard and inapproximable within k, which is the number of destination nodes. Thus, we design an approximate algorithm, called Recover Aware Edge Reduction Algorithm (RAERA), to solve the problem. The simulation results on real networks and large synthetic networks, together with the experiment on our SDN testbed with real YouTube traffic, all manifest that RST outperforms both SPT and ST. Also, the implementation of RAERA in SDN controllers shows that an RST can be returned within a few seconds and thereby is practical for SDN networks.
Non-black-box Techniques for Zero-Knowledge Protocols
Paper presented at the 35th International Cryptology Conference (2015).
Kai-Min Chung
- Institute of Information Science, Academia Sinica
This report summarizes our works on zero-knowledge (ZK) proofs in past years. ZK proofs is a fundamental primitive in cryptography that allows a party (called the Prover) to convince another party (called the Verifier) that a given claim is true without revealing any additional introduction. For example, an agent can prove that he has the right to enter a building without revealing his identity or password. Paradoxical as it may sound, it is extremely useful and has pervasive applications in cryptography.
Most ZK constructions are “black-box,” but black-box constructions cannot achieve several stronger notions of ZK proofs (see Figures). Achieving such notions are often long-standing open problems. Our works develop non-black-box techniques to bypass such limit, and achieve the following two notions of ZK proofs: (i) constant round concurrent ZK proofs from indistinguishability obfuscation (the paper cited below), and (ii) simultaneously resettable ZK proofs from the minimal assumption of one-way functions (published in FOCS 2013).